📖 例題
このサンプルの問題6は、「繰り返しの中に繰り返しがある」プログラムです。
外側の繰り返しのカウント変数「 i 」と、内側の繰り返しのカウント変数「 c 」を使って、掛け算の九九の計算を出力します。
📖 プログラム

これも、「ブロック構造の中にブロック構造がある」ので、「入れ子構造」です。
👩🏫繰り返しの中の繰り返し 👨🏫
サンプルの問題6では、「繰り返しの中に繰り返し」があります。
サンプルの問題5のときと同じように、ブロックの中のブロックを外のブロックと区別するための、「|」や「⎿ 」といった「インデント」を表す記号に注意するようにしてください。
また、同じように試験問題の中のプログラムに枠線を書き込んで、どこまでがブロックの中なのかを明確にしておくといいでしょう。

このような「二重の繰り返し構造」の場合、特に繰り返すごとに変数の値がどのように変化するのかをイメージするのが難しくなります。
考え方としては、「外側の繰り返しブロックが1回繰り返すごとに、内側の繰り返しブロックが指定回数繰り返す」と覚えておいてください。
それで、このサンプル問題の場合、外側の繰り返しのカウント変数「 i 」が1増えるたびに、内側の繰り返しのカウント変数「 c 」は「1から9」まで毎回変化します。
これも表にして考えると、わかりやすくなります。
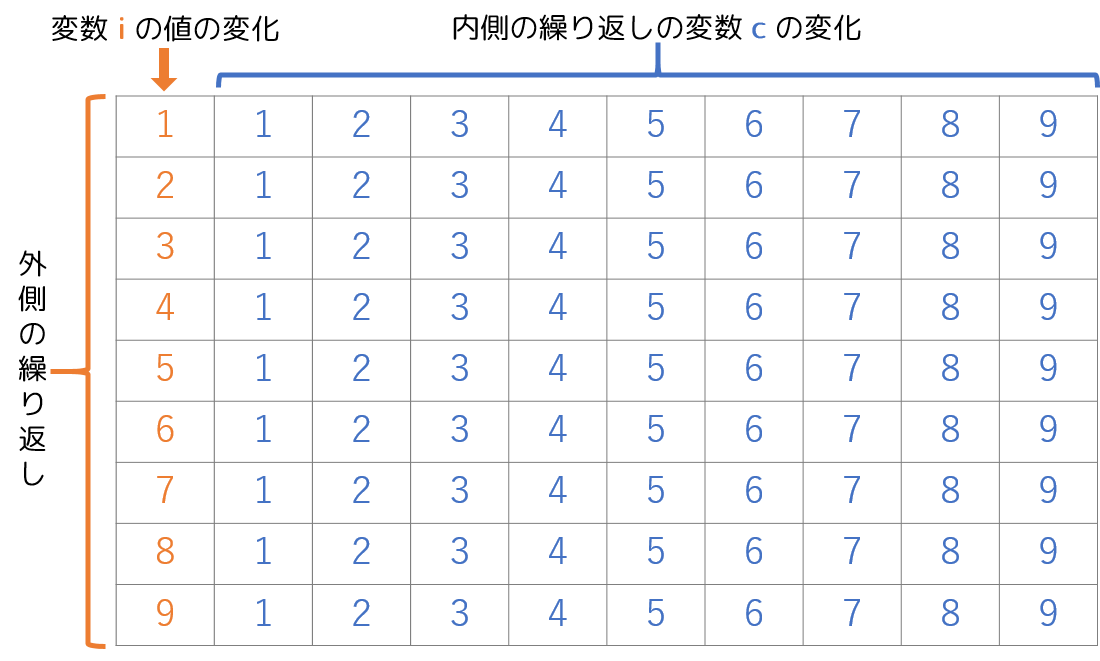
この表のように、外側の繰り返しが1ずつ増えながら繰り返すたびに、内側の繰り返しも1ずつ増えながら「1から9」まで毎回変化していきます。
それで、外側の変数の値と内側の変数の値を掛け合わせることで、掛け算の九九の計算ができることになります。
では、実際にプログラムを実行して確かめてみてください。「表示する( )」を実行するたびに改行されてしまいますので、計算結果は縦に並べて表示されます。
🧭 使用例
💻1
1から50までの範囲の数値を順に調べて、素数なら「素数です。」と表示するプログラムです。
「回数を指定する」繰り返しの中に、「条件を指定する」繰り返しがあります。
また、内側の繰り返しの中に「条件分岐」があります。
2つのカウント変数の値がどのように変化するかイメージしながら、なぜこのプログラムで素数の判定ができるのかを考えてみてください。

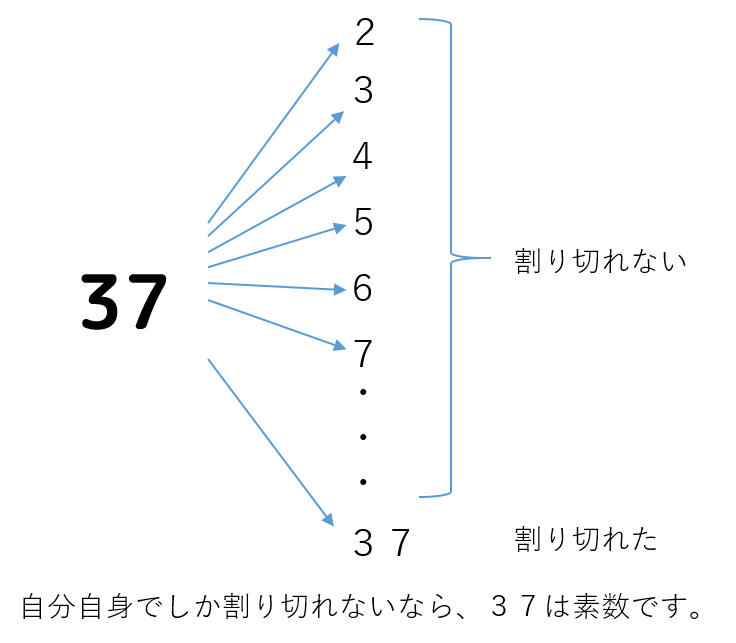
「素数」とは、「2以上の自然数で、1とその数自身の2つしか正の約数を持たない数」のことでした。
ある数値が素数かどうかを判断するには、「2からその数値まで順に割っていき、その数値でしか割り切れないならその数値は素数」と判断できます。
📖 解説
👩🏫
- 1から50までの範囲の数値を順番に調べます。
- i を 2 から 50 まで 1 ずつ増やしながら繰り返す:(外側の繰り返し)
「0」と「1」は素数ではないので、2から50までの範囲の数値を調べます。 - c = 2
素数を調べるには、2からその数値まで順に割っていくので、「c」の値は2から始めます。 - c <= i の間繰り返す:(内側の繰り返し)
調べたい「i」の値が素数かどうかを調べます。
「c」の値を、2から「i」まで「c <= i の間」繰り返し、「iをcで割り切れるか」判断しています。 - もし i % c == 0 ならば:
「i % c == 0」は余りが0だった、つまり「iをcで割り切れた」ということです。
割り切れたのならば次に素数かどうか判定します。割り切れたときの「c」の値と「i」の値が同じであれば素数です。 - もし i != c ならば:
「iとcの値が異なる」ならば、繰り返しの途中で「i」自身以外の値で割り切れたことになり「i」は素数ではないということになります。 - c = i
割り切れる数が繰り返しの途中で見つかった場合、内側の繰り返しを終了させるために繰り返しの条件が「false」となるよう「i」の値を「c」に代入します。
(例)調べたい数値「i」が6、「c」が3の時、6は3で割り切れるので素数ではない
➔「c = i」で「i」は6、「c」も6になる
➔10行目で「c」は7になると「c>i」となり、条件に満たないため内側の繰り返しが終了 - そうでなければ:
つまり、「iとcの値が同じ」ならば、「i」を割り切れたのは自分自身ということになるので素数! - 表示する( i , "は素数です。" )
「iは素数です。」と表示する処理が実行されることになります。 - c = c + 1
「c」のカウントアップをします。 - 表示する( "終わり" )
最後に「終わり」を表示させています。
💡 ポイント
- 「外側の繰り返しブロックが1回繰り返すごとに、内側の繰り返しブロックが指定回数繰り返す」と覚えておく。
- カウント変数の値の変化を表にすると分かりやすくなる。