📖 例題
このサンプルの問題8は、ログインを判定するプログラムです。
名前とパスワードが、それぞれ登録されている値と一致するかどうかを判定し、一致していれば「ログイン成功」と表示します。
📖 プログラム

構造としては条件分岐構造ですが、条件式のところに注目してください。
👩🏫 論理演算 👨🏫
このサンプルの問題8の中には、条件式が3箇所にあります。オレンジの枠で囲っている部分です。

これまでと違い、条件式がそれぞれ2つ書かれていて、それぞれの条件式の間には「or」と「and」の文字があります。
このような条件式を「論理演算」といいます。
「or」は、「論理和」を意味していて、「または」と言い換えるとわかりやすいでしょう。
また、「and」は、「論理積」を意味していて、「かつ」と言い換えるとわかりやすいでしょう。
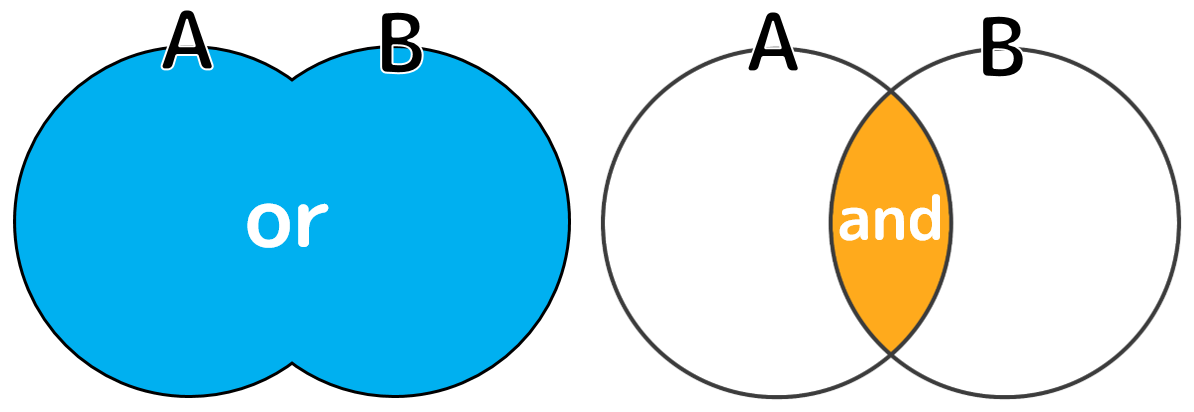
条件式が「or」でつながっている場合は、どちらか一方の条件式が「true」と評価されれば、その条件式全体も「true」と評価されます。
また、条件式が「and」でつながっている場合は、両方の条件式が「true」と評価されるとき、その条件式全体も「true」と評価されます。
では、実際に以下のサンプルの問題8を実行してみてください。
では、なぜこのような結果になったのか、プログラムを部分的に取り出して考えることにしましょう。
4行目では、条件式が「or」でつなげられていますから、変数「namae」の値が「スズキ」または「サトウ」のどちらかの場合に「true」と評価されることになります。
そして、変数「namae」には、文字列「サトウ」が代入されていますから、この条件全体の判定は「true」となります。
では、4行目の条件式だけを取り出して、ほんとうにそうなるのか確認してみることにしましょう。
確かに「true」と表示されましたね。
次に、以下の(1)と(2)の条件判定に入っていくことになるのですが、この場合2つの条件式が「and」でつなげられていますから、両方の条件判定が「true」のときに条件全体が「true」と判定されることになります。
(1) namae == "スズキ" and pasuwado == "eSj7mL6"
(2) namae == "サトウ" and pasuwado == "Rc29Xb4"
変数「namae」の値は「サトウ」でしたから、7行目の(2)の条件判定が行われます。
このとき、変数「pasuwado」に最初に代入されている値は「Et35m8k」でした。
それで、変数「pasuwado」の値と文字列「Rc29Xb4」は等しくないので、この条件式は「false」と評価されることになります。
そのため、(2)の条件判定では、一方の判定結果が「true」ではないために、条件全体の評価は「false」となります。
では、サンプルの問題8の7行目の条件式だけを取り出して、この点も確かめてみることにしましょう。
サンプルの問題8の7行目の条件判定は、確かに「false」となることが、これでわかりましたでしょうか。
そのため、サンプルの問題8の9行目の「そうでなければ:」の中の処理が実行されることになりますから、最終結果は「ログインに失敗しました。」と表示されます。
では、最終結果が「ログイン成功です。」と表示されるように、変数「namae」と「pasuwado」に最初に代入する値を変えて試してみてください。
🧭 使用例
💻1
天候と気温により、体育館内での運動をするかを判断するプログラムです。
天候が「晴れ または 雨」で、気温が「18度より低く または 30度より高い」場合は、「体育館で運動をする」と表示し、それ以外なら「屋外でも運動できる」と表示します。
📖 解説
👨🏫
条件式は、こうなっています。
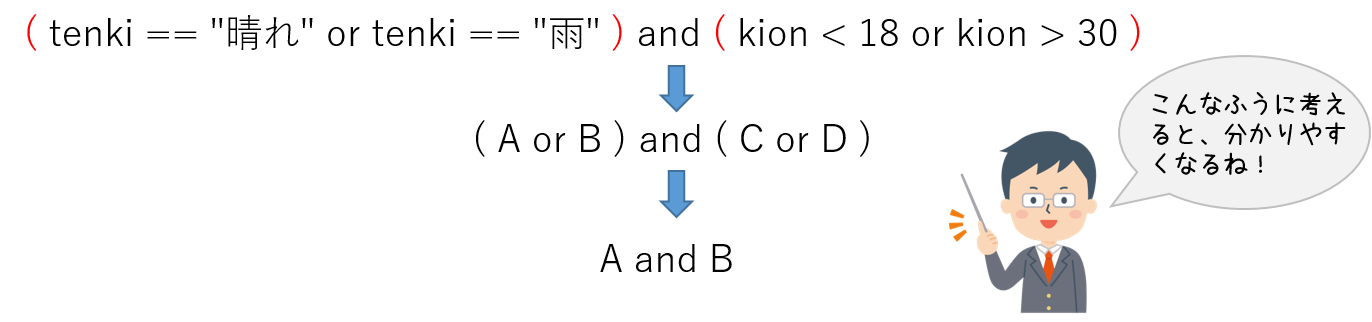
「tenki == "晴れ" or tenki == "雨" and kion < 18 or kion > 30」
とても複雑で分かりにくいですね。
このような場合は、「( )」を使って、条件式を分けて考えると、読みやすくなります。
👩🏫 not 👨🏫
論理演算には、「or」と「and」の他に、「not」というのがあります。
「not」は、条件式の否定を意味します。
それで、条件式の頭に「not」がつくと、以下のグレーの部分を意味するようになります。
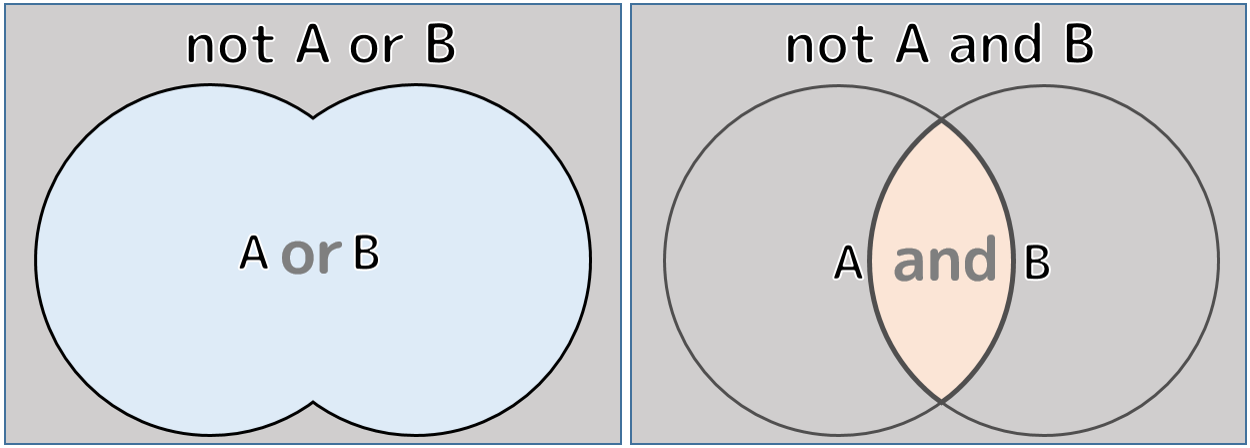
気温が「10度より低く または 30度より高い」という条件式の場合、2つの条件式全体を「( )」で囲み、先頭に「not」をつけると、「( )」の中の条件式全体を否定することになります。

上の2つの条件式が同じ結果になることを確かめてみましょう。
💡 ポイント
- 「or」と「and」を使って、条件式をつなぐことを「論理演算」という。
- 「or」は、「論理和」を意味していて、「または」と言い換えるとわかりやすい。
- 「and」は、「論理積」を意味していて、「かつ」と言い換えるとわかりやすい。
- 「not」は、条件式の否定を意味する。